On sensitivity of control chart for monitoring serially correlated data

Abstract

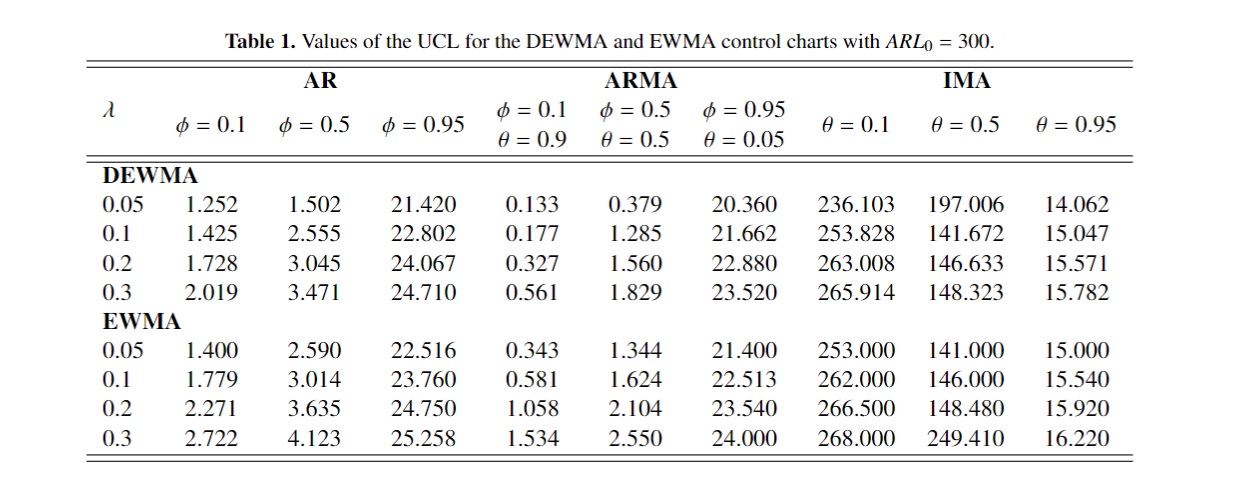
The normality and independent observations were designed for double exponentially weighted moving average (DEWMA) and exponentially weighted moving average (EWMA) control charts. DEWMA control chart was modified from the EWMA control chart. The performance of the control chart is measured in terms of the average run length (ARL) that is the average number of samples before getting an out-of-control signal. In a real application, data are dependent and non-normal observations. The exponential distribution has application in any area of the subject such as reliability theory, survival analysis and queuing theory. The purpose of this paper was to study DEWMA and EWMA control charts using the first-order autoregressive (AR(1)), the first-order autoregressive moving average (ARMA(1,1)) and the first-order integrated moving average (IMA(1,1)) models for an exponential distributed process variable to study the efficiency of detecting small process mean shift. A simulation using the R program was applied to study the ARL performances for DEWMA and EWMA control charts for the small process mean shift. Tables of ARLs are presented for the various process mean shift. All ARL at various sets of parameters of the control chart calculation was completed based on 10,000 replications for a scenario. The EWMA control chart is more efficient than the DEWMA control chart in the detection of small process mean shifts as it dependably gives smaller ARL values and quickly detects the process shift at various levels of correlation and shifts in the process mean. The application of serially correlated data in the control chart literature has achieved with wide suitability. The design and application of the DEWMA and EWMA control charts suggest a model in the detection of small process mean shift by process control employees.