สมาชิกของริงที่สอดคล้องกับการหารลงตัวบางรูปแบบ

ผู้แต่ง

  • กัญญาภัค ภัยแคล้ว Department of Mathematics, Faculty of Science and Technology, Nakhon Ratchasima Rajabhat University, Nakhon Ratchasima 30000, Thailand.
  • ญาณภัทร ทองร่อน Department of Mathematics, Faculty of Science and Technology, Nakhon Ratchasima Rajabhat University, Nakhon Ratchasima 30000, Thailand.
  • สุภัทรา เกิดมงคล Department of Mathematics, Faculty of Science and Technology, Nakhon Ratchasima Rajabhat University, Nakhon Ratchasima 30000, Thailand.
  • นิติภูมิ อัศวธิติสกุล Department of Mathematics, Faculty of Science and Technology, Nakhon Ratchasima Rajabhat University, Nakhon Ratchasima 30000, Thailand.
  • วราภรณ์ สุ่มมาตย์ General Education Affair, Thonburi University, Bangkok 10160, Thailand.

คำสำคัญ:

ริงสลับที่ที่มีเอกลักษณ์, การหารลงตัว, การหารยาว

บทคัดย่อ

กำหนดให้ R เป็นริงสลับที่ที่มีเอกลักษณ์ 1 และ m≥n เรานิยาม d∈R ที่สอดคล้องเงื่อนไขสองข้อต่อไปนี้
(bx^n-b) | (ax^m+d) ถ้า b | a และ
(bx^n-1) | (ax^m+d) ถ้า b^k | a
โดยที่ k คือผลหารจากการหาร m ด้วย n และ a, b∈R

เอกสารอ้างอิง

Burton D. M., (2011). Elementary Number Theory. New York: The McGraw-Hill Companies, Inc.

Durbin J. R. (2009). Modern Algebra: An Introduction (6th ed). New York: The University of Texas at Austin. John Wiley & Sons, Inc.

Lovett S. (2015). Abstract Algebra: Structures and Applications. New York: Chapman and Hall/CRC.

Malik D. S., Mordeson John M. and Sen M. K. (1997). Fundamentals of abstract algebra. New York: The McGraw-Hill Companies, Inc.

Niven I., Zuckerman H. S. and Montgomery H. L. (1991). An Introduction to the Theory of Numbers. New York: John Wiley & Sons, Inc.

Stitz C. and Zeager J. (2013). College Algebra. Retrieved Oct 10, 2022, from https://www.stitz-zeager.com/szca07042013.pdf.

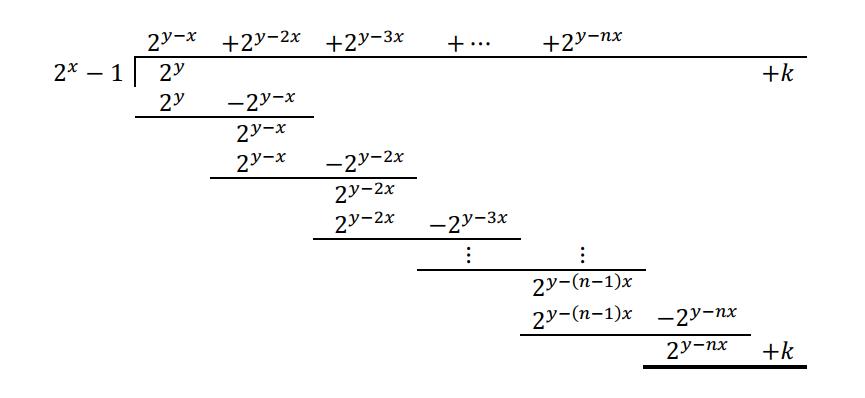
ดาวน์โหลด

เผยแพร่แล้ว

2024-06-07

รูปแบบการอ้างอิง

ภัยแคล้ว ก. ., ทองร่อน ญ. ., เกิดมงคล ส. ., อัศวธิติสกุล น., & สุ่มมาตย์ ว. (2024). สมาชิกของริงที่สอดคล้องกับการหารลงตัวบางรูปแบบ. วารสารวิจัย วิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยราชภัฏนครราชสีมา, 9(1), 1–7. สืบค้น จาก https://ph02.tci-thaijo.org/index.php/sciencenrrujournal/article/view/250431

ฉบับ

ปีที่ 9 ฉบับที่ 1 (2024): มกราคม-มิถุนายน : วารสารวิจัย วิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยราชภัฏนครราชสีมา

ประเภทบทความ

Research Articles

สัญญาอนุญาต

ลิขสิทธิ์ (c) 2024 วารสารวิจัย วิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยราชภัฏนครราชสีมา

Creative Commons License

อนุญาตภายใต้เงื่อนไข Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

เนื้อหาและข้อมูลในบทความที่ลงตีพิมพ์ในวารสารวิจัย วิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยราชภัฏนครราชสีมา ถือเป็นข้อคิดเห็นและความรับผิดชอบของผู้เขียนบทความโดยตรงซึ่งกองบรรณาธิการวารสาร ไม่จำเป็นต้องเห็นด้วย หรือร่วมรับผิดชอบใด ๆ
บทความ ข้อมูล เนื้อหา รูปภาพ ฯลฯ ที่ได้รับการตีพิมพ์ในวารสารวิจัย วิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยราชภัฏนครราชสีมา ถือเป็นลิขสิทธิ์ของวารสารวิจัย วิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยราชภัฏนครราชสีมา หากบุคคลหรือหน่วยงานใดต้องการนำทั้งหมดหรือส่วนหนึ่งส่วนใดไปเผยแพร่ต่อหรือเพื่อกระทำการใด ๆ จะต้องได้รับอนุญาตเป็นลายลักอักษรจากวารสารวิจัย วิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยราชภัฏนครราชสีมา ก่อนเท่านั้น