Enhancing linear regression through neighbor-based similarity analysis

Abstract

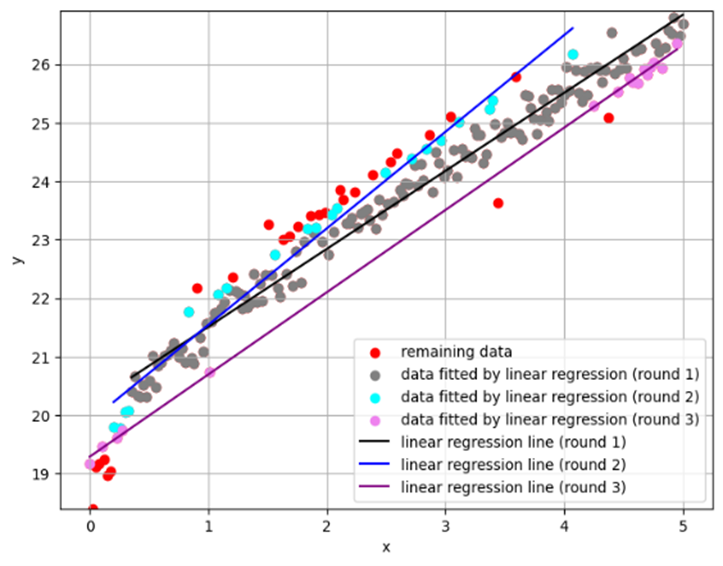
When working with real-world datasets characterized by complex and non-linear relationships, the limitations of non-complex machine learning models like linear regression become evident. In response to addressing this technical problem, we propose a novel algorithm to enhance linear regression without the necessity of complex mathematical or statistical expressions. Instead, the algorithm segments data into multiple subgroups or neighbors, each with its own best-fitting line. The primary objective of this approach is to enable more accurate predictions for unseen data points by utilizing the most similar neighbors and their corresponding linear regression lines, with the support of k-nearest neighbors. Empirical evidence from three publicly available housing price datasets demonstrates the algorithm’s effectiveness in improving traditional linear regression models.