Linear Ensemble Algorithm: A Novel Meta-Heuristic Approach for Solving Constrained Engineering Problems
Main Article Content
Abstract
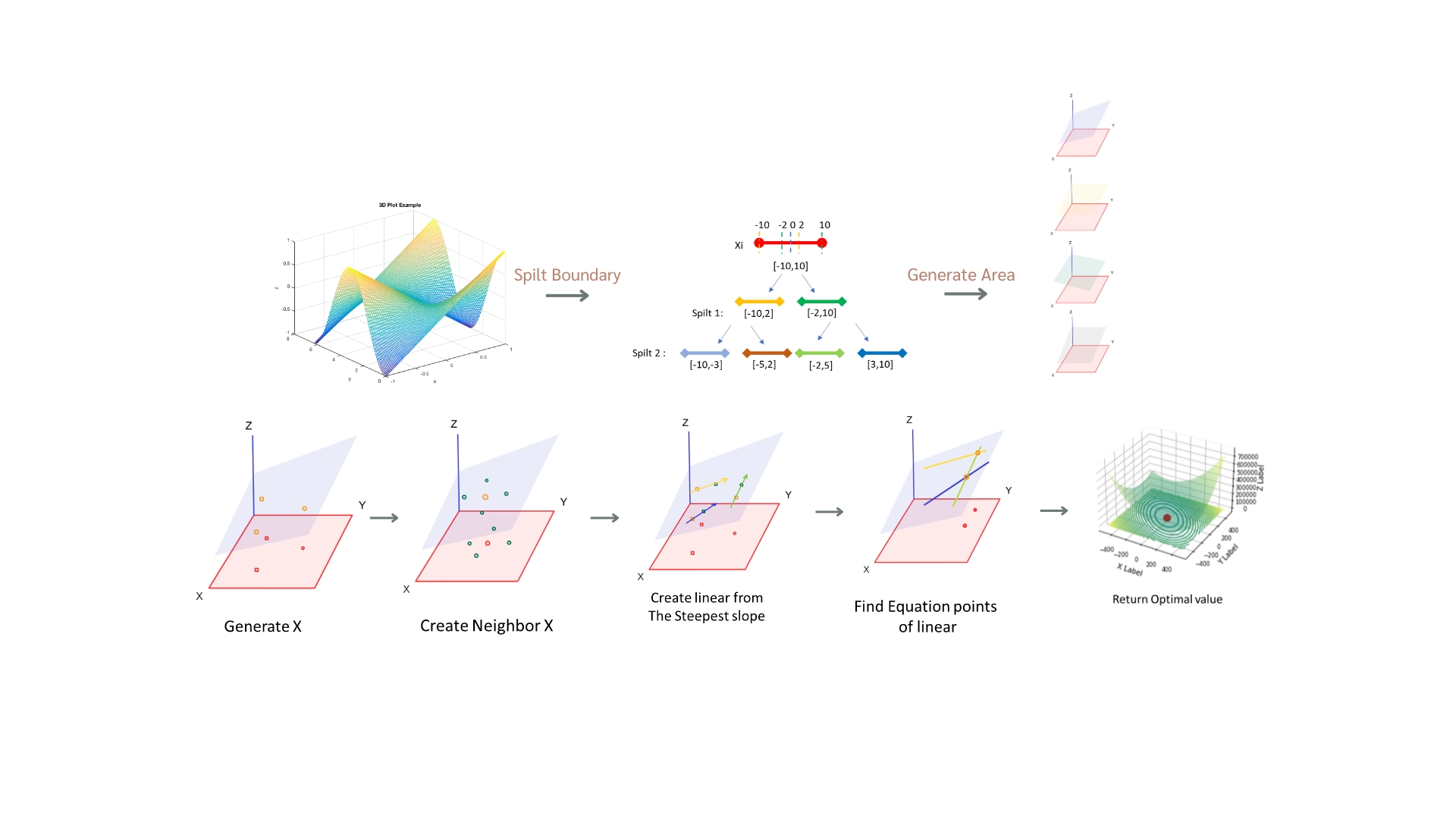
This research This study presents the Linear Ensemble Algorithm (LEAL), which couples evolutionary search with local, linear regression–based surrogates and a neighbor-guided linear combination scheme for constrained engineering problems and standard benchmarks. For single-objective problems, LEAL frequently attains or closely approaches global optima on multimodal functions such as Rastrigin and Griewank, yielding ~55–85% lower mean error than GA, DE, and PSO, and it can occasionally uncover best-known minima in engineering tasks (e.g., Pressure Vessel), indicating an ability to exploit intricate design trade-offs. For multi-objective problems, LEAL generates feasible Pareto fronts but generally trails NSGA-II in convergence and efficiency, exhibiting higher GD⁺, longer runtimes, and greater memory usage (often by one to two orders of magnitude). These outcomes reflect the computational overhead of maintaining local surrogate ensembles: while LEAL can produce high-quality solutions, its average performance, runtime, and memory footprint are often inferior to lightweight baselines. Comparisons with CMA-ES, Bayesian Optimization, and SSA-NSGA-II confirm the same trade-offs. Overall, LEAL is a robust yet computationally intensive option best suited when ultimate solution quality outweighs runtime; future work will focus on improving efficiency, streamlining ensemble components, and extending applicability to large-scale and dynamic problems.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
References
Goldberg, D. E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989.
Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Proc. IEEE Int. Conf. Neural Networks 1995, 4, 1942–1948. https://doi.org/10.1109/ICNN.1995.488968
Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6(2), 182–197. https://doi.org/10.1109/4235.996017
Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Global Optim. 1997, 11(4), 341–359. https://doi.org/10.1023/A:1008202821328
Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9(2), 159–195. https://doi.org/10.1162/106365601750190398
Glover, F.; Kochenberger, G. A., Eds. Handbook of Metaheuristics; Springer: Boston, MA, USA, 2003. https://doi.org/10.1007/b101874
Yang, X. S.; Deb, S.; Fong, S. Metaheuristic Algorithms: Optimal Balance of Intensification and Diversification. Appl. Math. Inf. Sci. 2011, 5(3), 236–254. Available online: https://www.naturalspublishing.com/Article.asp?ArtcID=1637 (accessed 4 Sep 2025).
Blum, C.; Roli, A. Metaheuristics in Combinatorial Optimization: Overview and Conceptual Comparison. ACM Comput. Surv. 2003, 35(3), 268–308. https://doi.org/10.1145/937503.937505
Coello-Coello, C. A. Theoretical and Numerical Constraint-Handling Techniques Used with Evolutionary Algorithms: A Survey of the State of the Art. Comput. Methods Appl. Mech. Eng. 2002, 191(11–12), 1245–1287. https://doi.org/10.1016/S0045-7825(01)00323-1
Hansen, N. The CMA Evolution Strategy: A Tutorial. arXiv 2016, arXiv:1604.00772. Available online: https://arxiv.org/abs/1604.00772 (accessed 4 Sep 2025).
Arnold, D. V.; Hansen, N. A (1+1)-CMA-ES for Constrained Optimisation. Proc. Genetic and Evolutionary Computation Conference (GECCO) 2012, 297–304. https://doi.org/10.1145/2330163.2330207
Sakamoto, N.; Akimoto, Y. Adaptive Ranking Based Constraint Handling for Explicitly Constrained Black-Box Optimization. In Parallel Problem Solving from Nature – PPSN XV; Auger, A., Fonseca, C., Lourenço, N., Eds.; Springer: Cham, Switzerland, 2018; pp. 72–83. https://doi.org/10.1007/978-3-319-99259-4_6
Morinaga, S.; Akimoto, Y. Safe Control with CMA-ES by Penalizing Unsafe Search Directions. Proc. Genetic and Evolutionary Computation Conference (GECCO) 2024, 344–352. https://doi.org/10.1145/3638529.3654047
He, X.; He, Y.; He, Z.; Yang, S. KbP-LaF-CMAES: Knowledge-based Principal Landscape-aware Feasible CMA-ES for Constrained Optimization. Inf. Sci. 2024, 670, 119–141. https://doi.org/10.1016/j.ins.2024.01.088
Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R. P.; de Freitas, N. Taking the Human out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104(1), 148–175. https://doi.org/10.1109/JPROC.2015.2494218
Snoek, J.; Larochelle, H.; Adams, R. P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. (NeurIPS) 2012, 25, 2951–2959. https://dl.acm.org/doi/10.5555/2999325.2999464
Eriksson, D.; Pearce, M.; Gardner, J.; Turner, R.; Poloczek, M. Scalable Constrained Bayesian Optimization. Proc. Int. Conf. Machine Learning (ICML) 2021, 139, 2949–2958. https://proceedings.mlr.press/v139/eriksson21a.html.
Regli, J. B.; Shoemaker, C. A. Hybrid Bayesian Optimization and IPOPT for Constrained Black-Box Optimization. Struct. Multidiscip. Optim. 2025, 66(2), 45–61. https://doi.org/10.1007/s00158-025-03729-9
Daulton, S.; Balandat, M.; Bakshy, E. Parallel Bayesian Optimization of Multiple Noisy Objectives with Expected Hypervolume Improvement. Adv. Neural Inf. Process. Syst. (NeurIPS) 2020, 33, 752–764. https://proceedings.neurips.cc/paper/2020/hash/6b493230205f780e1bc26945df7481e5-Abstract.html.
Deb, K. An Efficient Constraint Handling Method for Genetic Algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186(2–4), 311–338. https://doi.org/10.1016/S0045-7825(99)00389-8
Lim, D.; Ong, Y. S.; Jin, Y.; Sendhoff, B. A Study on Metamodeling Techniques, Ensembles, and Multi-Surrogates in Evolutionary Computation. Proc. Genetic and Evolutionary Computation Conference (GECCO) 2007, 1288–1295. https://doi.org/10.1145/1276958.1277180
Ong, Y. S.; Nair, P. B.; Keane, A. J. Evolutionary Optimization of Computationally Expensive Problems via Surrogate Modeling. AIAA J. 2003, 41(4), 687–696. https://doi.org/10.2514/2.2010
Jin, Y. A Comprehensive Survey of Fitness Approximation in Evolutionary Computation. Soft Comput. 2005, 9(1), 3–12. https://doi.org/10.1007/s00500-003-0328-6
Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. https://doi.org/10.1109/ACCESS.2020.2990567
Brockhoff, D.; Trautmann, H. Pysamoo: Surrogate-Assisted Multi-Objective Optimization in Python. Proc. Genetic and Evolutionary Computation Conference (GECCO Companion) 2021, 1840–1847. https://doi.org/10.1145/3449726.3463204
Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, É. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. http://jmlr.org/papers/v12/pedregosa11a.html
Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective Selection Based on Dominated Hypervolume. Eur. J. Oper. Res. 2007, 181(3), 1653–1669. https://doi.org/10.1016/j.ejor.2006.08.008. (Least HV contribution / HV-based survival) https://doi.org/10.1016/j.ejor.2006.08.008
Ishibuchi, H.; Masuda, H.; Tanigaki, Y.; Nojima, Y. Modified Distance Calculation in Generational Distance and Inverted Generational Distance. In Evolutionary Multi-Criterion Optimization (EMO 2015); Lecture Notes in Computer Science, Vol. 9019; Springer: Cham, 2015; pp 110–125. https://doi.org/10.1007/978-3-319-15892-1_8
Daulton, S.; Balandat, M.; Bakshy, E. Differentiable Expected Hypervolume Improvement for Parallel Multi-Objective Bayesian Optimization. NeurIPS 2020, 33, 9851–9864.
Daulton, S.; Balandat, M.; Bakshy, E. Noisy Expected Hypervolume Improvement for Multi-Objective Bayesian Optimization. NeurIPS 2021, 34, 24368–24381.
Liu, S.; Gong, M.; Zhang, Q.; Jin, Y. Surrogate-Assisted Evolutionary Algorithms for Expensive Optimization: A Recent Survey. IEEE Comput. Intell. Mag. 2024, 19(2), 45–73.
Yu, L.; Wang, H.; Jin, Y. Surrogate-Assisted Differential Evolution: A Survey. Swarm Evol. Comput. 2025, 85, 101507. https://doi.org/10.1016/j.swevo.2025.101879